整体架构
HashMap 底层的数据结构主要是:数组 + 链表 + 红黑树。其中当链表的长度大于等于 8 时,链表会转化成红黑树,当红黑树的大小小于等于 6 时,红黑树会转化成链表,整体的数据结构如下:
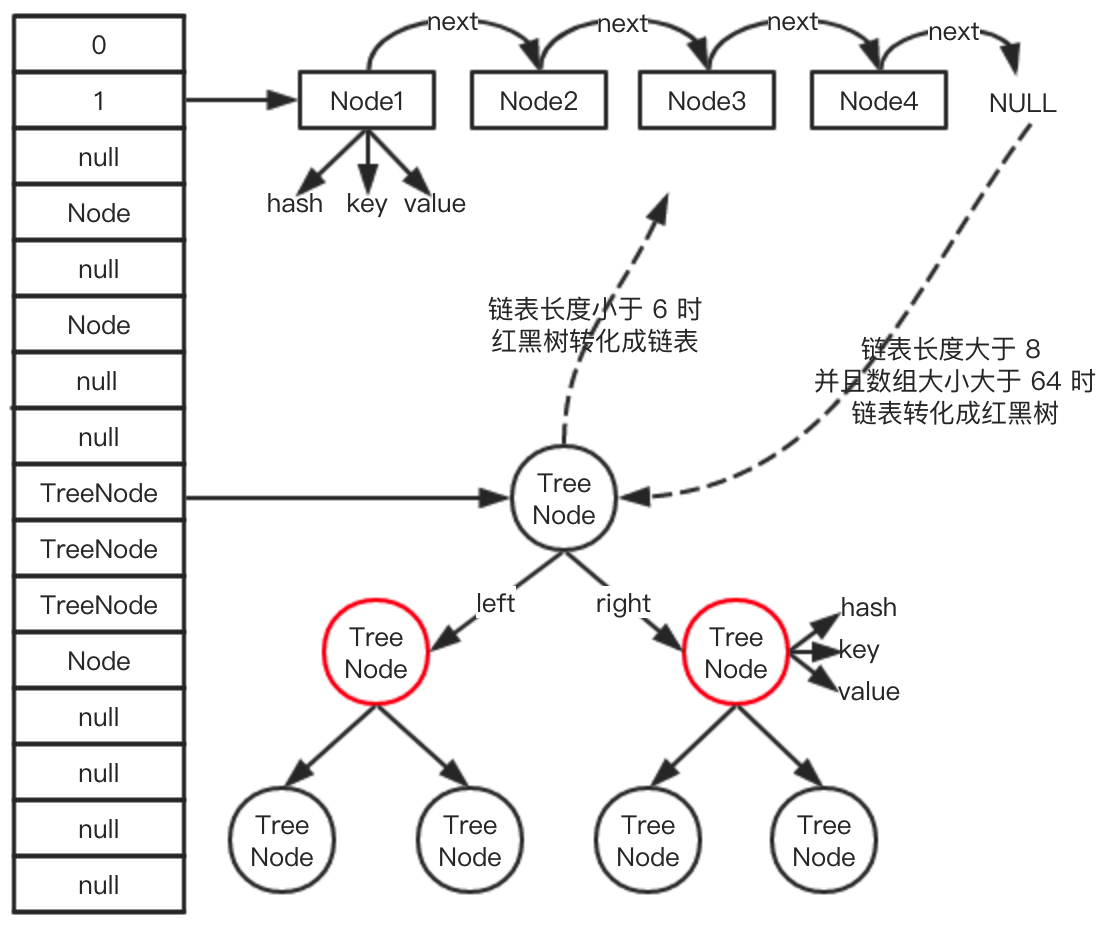
图中左边竖着的是 HashMap 的数组结构,数组的元素可能是单个 Node,也可能是个链表,也可能是个红黑树,比如数组下标索引为 2 的位置就是一个链表,下标索引为 9 的位置对应的就是红黑树,具体细节我们下文再说。
类注释
从 HashMap 的类注释中,我们可以得到如下信息:
- 允许 null 值,不同于 HashTable ,是线程不安全的;
- load factor(影响因子) 默认值是 0.75, 是均衡了时间和空间损耗算出来的值,较高的值会减少空间开销(扩容减少,数组大小增长速度变慢),但增加了查找成本(hash 冲突增加,链表长度变长),不扩容的条件:数组容量 > 需要的数组大小 /load factor;
- 如果有很多数据需要储存到 HashMap 中,建议 HashMap 的容量一开始就设置成足够的大小,这样可以防止在其过程中不断的扩容,影响性能;
- HashMap 是非线程安全的,我们可以自己在外部加锁,或者通过 Collections#synchronizedMap 来实现线程安全,Collections#synchronizedMap 的实现是在每个方法上加上了 synchronized 锁;
- 在迭代过程中,如果 HashMap 的结构被修改,会快速失败。
常见属性
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;
static final int MAXIMUM_CAPACITY = 1 << 30;
static final float DEFAULT_LOAD_FACTOR = 0.75f;
static final int TREEIFY_THRESHOLD = 8;
static final int UNTREEIFY_THRESHOLD = 6;
static final int MIN_TREEIFY_CAPACITY = 64;
transient int modCount;
transient int size;
transient Node<K,V>[] table;
int threshold;
static class Node<K,V> implements Map.Entry<K,V> {
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
|
新增
新增 key,value 大概的步骤如下:
1
2
3
4
5
6
7
| 1.空数组有无初始化,没有的话初始化;
2.如果通过 key 的 hash 能够直接找到值,跳转到 6,否则到 3;
3.如果 hash 冲突,两种解决方案:链表 or 红黑树;
4.如果是链表,递归循环,把新元素追加到队尾;
5.如果是红黑树,调用红黑树新增的方法;
6.通过 2、4、5 将新元素追加成功,再根据 onlyIfAbsent 判断是否需要覆盖;
7.判断是否需要扩容,需要扩容进行扩容,结束。
|
我们来画一张示意图来描述下:
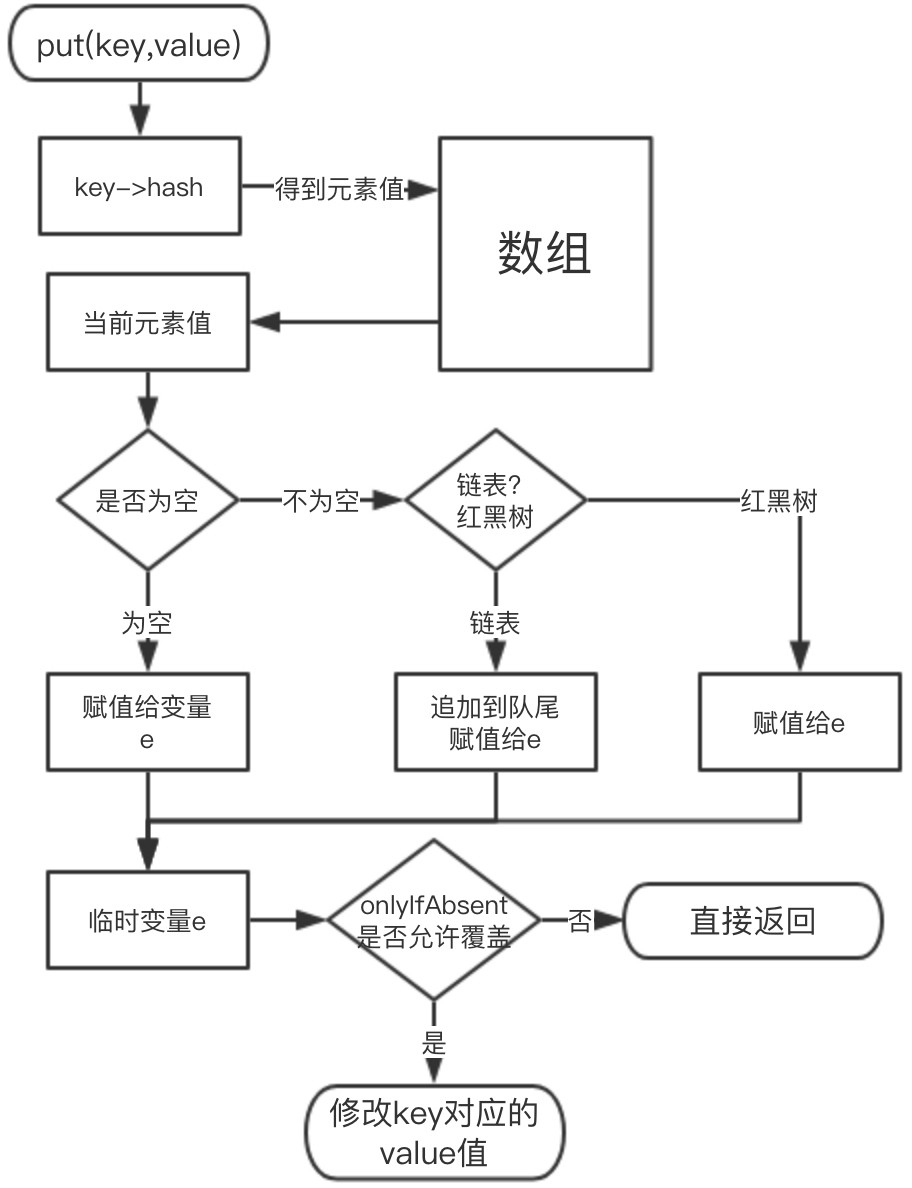
代码细节如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
|
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1)
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
if (e != null) {
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
|
新增的流程上面应该已经表示很清楚了,接下来我们来看看链表和红黑树新增的细节:
链表的新增
链表的新增比较简单,就是把当前节点追加到链表的尾部,和 LinkedList 的追加实现一样的。
当链表长度大于等于 8 时,此时的链表就会转化成红黑树,转化的方法是:treeifyBin,此方法有一个判断,当链表长度大于等于 8,并且整个数组大小大于 64 时,才会转成红黑树,当数组大小小于 64 时,只会触发扩容,不会转化成红黑树,转化成红黑树的过程也比较简单。
为什么是8呢,这个答案在源码中注释有说,中文翻译过来大概的意思是:
链表查询的时间复杂度是 O (n),红黑树的查询复杂度是 O (log (n))。在链表数据不多的时候,使用链表进行遍历也比较快,只有当链表数据比较多的时候,才会转化成红黑树,但红黑树需要的占用空间是链表的 2 倍,考虑到转化时间和空间损耗,所以我们需要定义出转化的边界值。
在考虑设计 8 这个值的时候,我们参考了泊松分布概率函数,由泊松分布中得出结论,链表各个长度的命中概率为:
1
2
3
4
5
6
7
8
9
| * 0: 0.60653066
* 1: 0.30326533
* 2: 0.07581633
* 3: 0.01263606
* 4: 0.00157952
* 5: 0.00015795
* 6: 0.00001316
* 7: 0.00000094
* 8: 0.00000006
|
意思是,当链表的长度是 8 的时候,出现的概率是 0.00000006,不到千万分之一,所以说正常情况下,链表的长度不可能到达 8 ,而一旦到达 8 时,肯定是 hash 算法出了问题,所以在这种情况下,为了让 HashMap 仍然有较高的查询性能,所以让链表转化成红黑树,我们正常写代码,使用 HashMap 时,几乎不会碰到链表转化成红黑树的情况,毕竟概念只有千万分之一。
红黑树新增节点过程
- 1.首先判断新增的节点在红黑树上是不是已经存在,判断手段有如下两种:
- 1.1如果节点没有实现 Comparable 接口,使用 equals 进行判断;
- 1.2.如果节点自己实现了 Comparable 接口,使用 compareTo 进行判断。
- 2.新增的节点如果已经在红黑树上,直接返回;不在的话,判断新增节点是在当前节点的左边还是右边,左边值小,右边值大;
- 3.自旋递归 1 和 2 步,直到当前节点的左边或者右边的节点为空时,停止自旋,当前节点即为我们新增节点的父节点;
- 4.把新增节点放到当前节点的左边或右边为空的地方,并于当前节点建立父子节点关系;
- 5.进行着色和旋转,结束。
具体源码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
|
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
int h, K k, V v) {
Class<?> kc = null;
boolean searched = false;
TreeNode<K,V> root = (parent != null) ? root() : this;
for (TreeNode<K,V> p = root;;) {
int dir, ph; K pk;
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
return p;
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0) {
if (!searched) {
TreeNode<K,V> q, ch;
searched = true;
if (((ch = p.left) != null &&
(q = ch.find(h, k, kc)) != null) ||
((ch = p.right) != null &&
(q = ch.find(h, k, kc)) != null))
return q;
}
dir = tieBreakOrder(k, pk);
}
TreeNode<K,V> xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) {
Node<K,V> xpn = xp.next;
TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);
if (dir <= 0)
xp.left = x;
else
xp.right = x;
xp.next = x;
x.parent = x.prev = xp;
if (xpn != null)
((TreeNode<K,V>)xpn).prev = x;
moveRootToFront(tab, balanceInsertion(root, x));
return null;
}
}
}
|
红黑树的新增,要求大家对红黑树的数据结构有一定的了解。面试的时候,一般只会问到新增节点到红黑树上大概是什么样的一个过程,着色和旋转的细节不会问,因为很难说清楚,但我们要清楚着色指的是给红黑树的节点着上红色或黑色,旋转是为了让红黑树更加平衡,提高查询的效率,总的来说都是为了满足红黑树的 5 个原则:
- 节点是红色或黑色
- 根是黑色
- 所有叶子都是黑色
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点
- 从每个叶子到根的所有路径上不能有两个连续的红色节点
查找
HashMap 的查找主要分为以下三步:
- 根据 hash 算法定位数组的索引位置,equals 判断当前节点是否是我们需要寻找的 key,是的话直接返回,不是的话往下。
- 判断当前节点有无 next 节点,有的话判断是链表类型,还是红黑树类型。
- 分别走链表和红黑树不同类型的查找方法。
链表查找的关键代码是:
1
2
3
4
5
6
7
8
9
|
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
|
红黑树查找的代码很多,我们大概说下思路,实际步骤比较复杂,可以去 github 上面去查看源码:
- 从根节点递归查找;
- 根据 hashcode,比较查找节点,左边节点,右边节点之间的大小,根本红黑树左小右大的特性进行判断;
- 判断查找节点在第 2 步有无定位节点位置,有的话返回,没有的话重复 2,3 两步;
- 一直自旋到定位到节点位置为止。
如果红黑树比较平衡的话,每次查找的次数就是树的深度。
文章作者:米兰
原始链接:https://blog.milanchen.site/posts/hashmap.html
版权声明:转载请声明出处

