椭圆曲线签名

ECDSA-secp256k1

以太坊数字签名算法使用的是椭圆曲线数字签名算法，英文简称ECDSA。
其中EC是“椭圆曲线”的简称，DSA是“数字签名算法”的简称。
椭圆曲线算法简单的说就是用X和Y坐标画一个曲线。
这个曲线怎么画，需要很多个参数来确定。
以太坊使用了一套叫secp256k1的参数确定了椭圆的形状。
所以，以太坊的椭圆曲线签名算法全称就是ECDSA-secp256k1。

相关概念

• 私钥：随机生成的32字节的二进制字符串。
• 公钥：由椭圆曲线算法ECDSA-secp256k1将私钥映射生成64字节的公钥。
• 地址：使用hash算法Keccak-256对公钥进行hash，将公钥转化为32字节，然后取最后的20字节作为账户地址。

总的来说名，就是私钥通过椭圆曲线算法可以计算出公钥和地址，私钥很重要。

假设Alice要给Bob发一个签名消息，而Bob需要验证该签名是否正确。

在ECDSA中，pubkey = prikey * G; (比如我的私钥是100，那么公钥就是100G)。

那么可能有同学就会问了，那么如果我知道公钥了，G点也是固定的，那么私钥不就逆向推出公钥/G嚒，其实不是这样的。
因为椭圆加密中的乘法和简单数学中的乘法是不太一样的，而且椭圆加密算法中没有除法这一个概念。

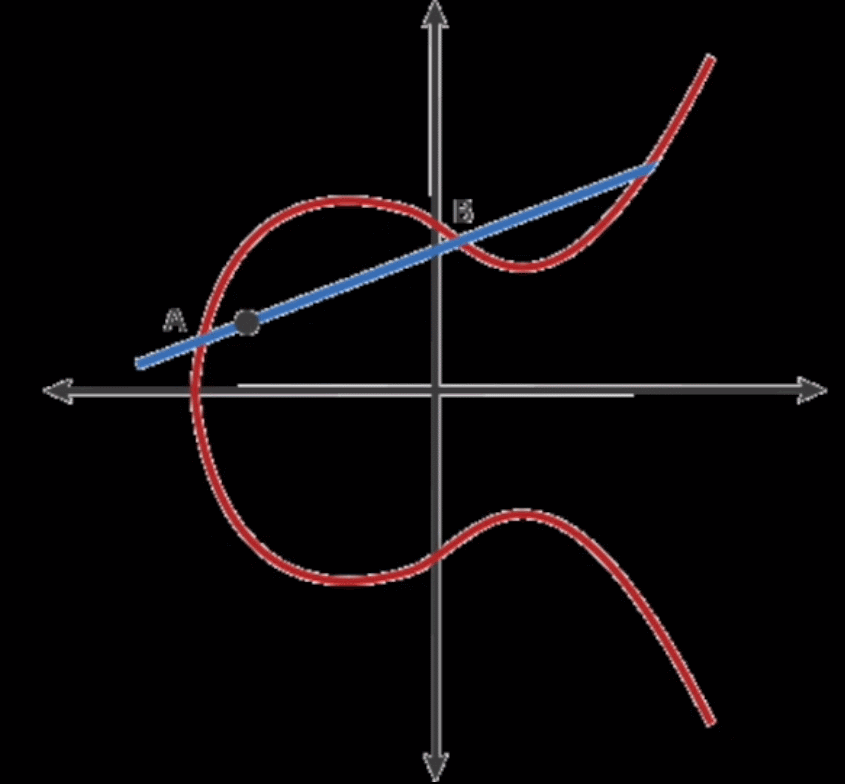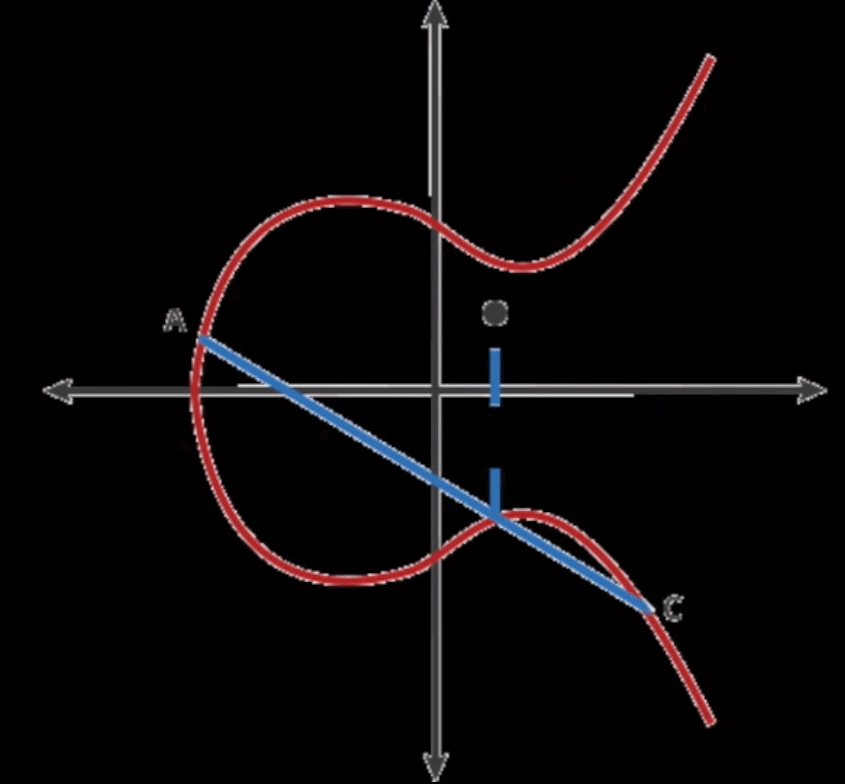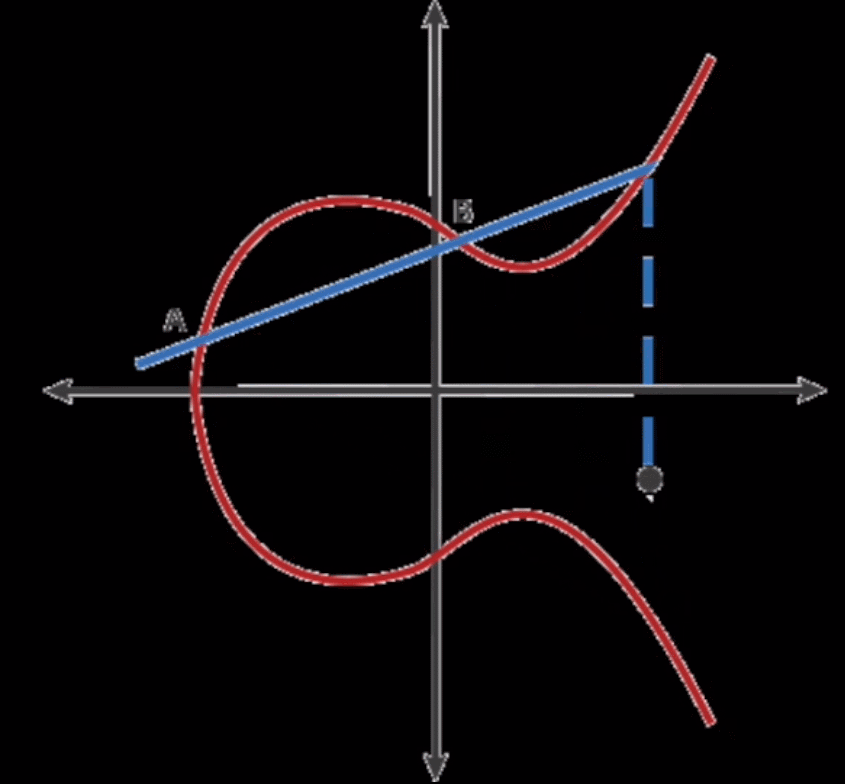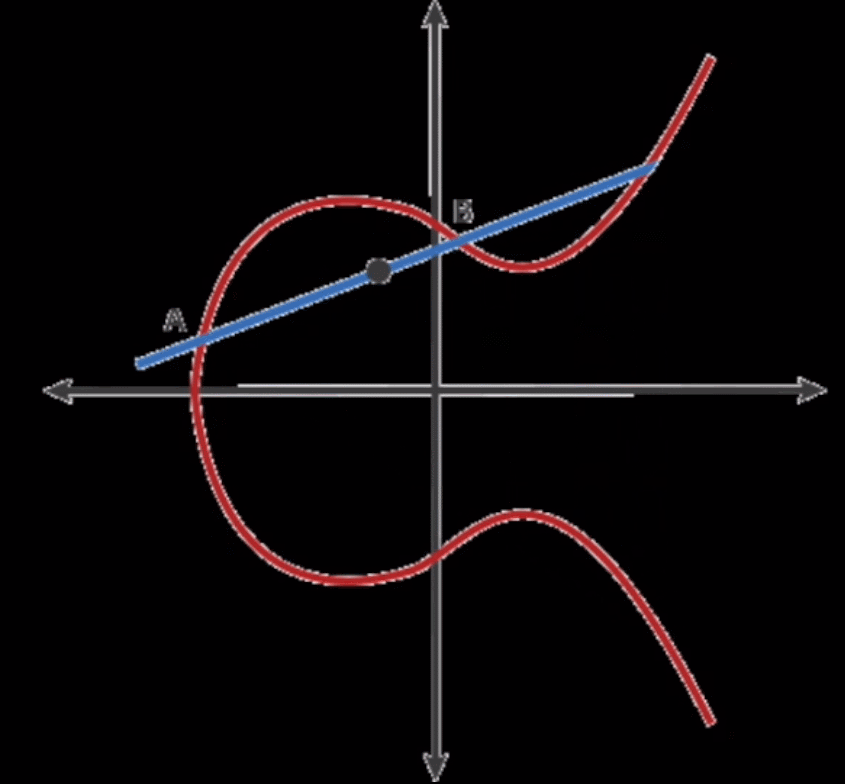
如上图所示，来看看乘法是怎么算的。
这里先说说加法吧，在椭圆加密运算中，A点加上B点是这么定义的：
经过A点和B点的直线会和椭圆加密曲线上的第三个点相交，这第三个点和X轴对称的点就是A+B的结果。

那么乘法怎么算呢，G * 2 = 2G = G + G，也就是在G点做切线和曲线相交的第三个点，第三个点对称之后就是2G，然后2G + G就是3G，3G + G就是4G。
所以椭圆加密曲线的乘法其实就是G点不断的相加。
可以想象一下，这个点从G点开始，在椭圆加密曲线中不断的反弹，反弹了私钥那么多次之后，最终达到终点，这个点就是公钥了。
所以我们无法从终点知道它反弹了多少次，是怎么样弹的，也就是说无法从公钥逆推出私钥。

可见从私钥->公钥->地址计算是很容易的，但是反过来计算是不可能的，这也就是非对称加密算法。

椭圆曲线涉及(CURVE, G, n)，其中CURVE表示椭圆曲线点域和几何方程；G就是上面提到的所有点倍积运算的基点；n是该椭圆曲线的可倍积阶数(multiplicative order)`，这里先留个坑，日后详细的研究，这里只做简单的介绍。
可参考：椭圆曲线数字签名算法理论

以太坊椭圆曲线签名

数字签名的生成

签名其实就是用私钥对消息的哈希进行加密。

// Sign calculates an ECDSA signature.
//
// This function is susceptible to chosen plaintext attacks that can leak
// information about the private key that is used for signing. Callers must
// be aware that the given hash cannot be chosen by an adversery. Common
// solution is to hash any input before calculating the signature.
//
// The produced signature is in the [R || S || V] format where V is 0 or 1.
// 最终会返回的签名是一个字节数组，按R / S / V的顺序排列
// 通过哈希和私钥计算ECDSA签名
func Sign(hash []byte, prv *ecdsa.PrivateKey) ([]byte, error) {
	if len(hash) != 32 {
		return nil, fmt.Errorf("hash is required to be exactly 32 bytes (%d)", len(hash))
	}
	if prv.Curve != btcec.S256() {
		return nil, fmt.Errorf("private key curve is not secp256k1")
	}
	sig, err := btcec.SignCompact(btcec.S256(), (*btcec.PrivateKey)(prv), hash, false)
	if err != nil {
		return nil, err
	}
	// Convert to Ethereum signature format with 'recovery id' v at the end.
	v := sig[0] - 27
	copy(sig, sig[1:])
	sig[64] = v
	return sig, nil
}

数字签名的验证

节点收到对方发来的消息和签名后，会先做一个“recover”的动作，用消息和签名推导出对方的公钥。再通过公钥，签名，消息的哈希值计算出一个叫“r”的值，这个r是签名的一部分，拿计算出来的r和签名中携带的r经行对比，如果一致就校验通过。

// Ecrecover returns the uncompressed public key that created the given signature.
// 通过消息的哈希和签名恢复公钥
func Ecrecover(hash, sig []byte) ([]byte, error) {
	pub, err := SigToPub(hash, sig)
	if err != nil {
		return nil, err
	}
	bytes := (*btcec.PublicKey)(pub).SerializeUncompressed()
	return bytes, err
}

// SigToPub returns the public key that created the given signature.
func SigToPub(hash, sig []byte) (*ecdsa.PublicKey, error) {
	// Convert to btcec input format with 'recovery id' v at the beginning.
	btcsig := make([]byte, 65)
	btcsig[0] = sig[64] + 27
	copy(btcsig[1:], sig)
	// 真实的实现调用了一个第三方的比特币的go项目，源码在vendor/github.com/bitcsuite/bitcd
	pub, _, err := btcec.RecoverCompact(btcec.S256(), btcsig, hash)
	return (*ecdsa.PublicKey)(pub), err
}

// VerifySignature checks that the given public key created signature over hash.
// The public key should be in compressed (33 bytes) or uncompressed (65 bytes) format.
// The signature should have the 64 byte [R || S] format.
// 通过公钥，哈希校验签名
func VerifySignature(pubkey, hash, signature []byte) bool {
	if len(signature) != 64 {
		return false
	}
	sig := &btcec.Signature{R: new(big.Int).SetBytes(signature[:32]), S: new(big.Int).SetBytes(signature[32:])}
	key, err := btcec.ParsePubKey(pubkey, btcec.S256())
	if err != nil {
		return false
	}
	// Reject malleable signatures. libsecp256k1 does this check but btcec doesn't.
	if sig.S.Cmp(secp256k1halfN) > 0 {
		return false
	}
	// crypto/ecdsa/ecdsa.go/Verify(pub *PublicKey, hash []byte, r, s *big.Int)
	// 计算出来的r和签名中携带的r经行对比
	return sig.Verify(hash, key)
}

椭圆曲线签名结果中r,s,v的定义

我们知道r，s，v是分别来自签名结果串。

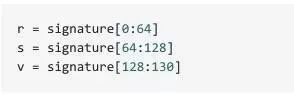
r为点的x坐标，s为点的y坐标，v坐标的奇偶检验标识符，27表示偶数y, 28表示奇数y。
这个具体可以参考：
What does v, r, s in eth_getTransactionByHash mean?
椭圆曲线签名算法的v的定义